跳转至

矩阵分解概述

推荐系统

介绍

随着互联网的发展，人们正处于一个信息爆炸的时代。相比于过去的信息匮乏，面对现阶段海量的信息数据，对信息的筛选和过滤成为了衡量一个系统好坏的重要指标。一个具有良好用户体验的系统，会将海量信息进行筛选、过滤，将用户最关注最感兴趣的信息展现在用户面前。这大大增加了系统工作的效率，也节省了用户筛选信息的时间。

搜索引擎的出现在一定程度上解决了信息筛选问题，但还远远不够。搜索引擎需要用户主动提供关键词来对海量信息进行筛选。当用户无法准确描述自己的需求时，搜索引擎的筛选效果将大打折扣，而用户将自己的需求和意图转化成关键词的过程本身就是一个并不轻松的过程。

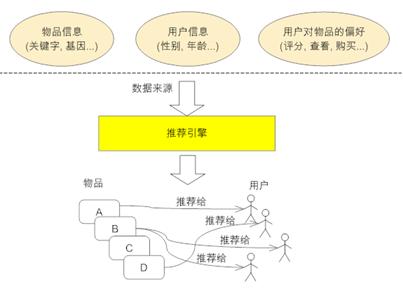
在此背景下，推荐系统出现了，推荐系统的任务就是解决上述的问题，联系用户和信息，一方面帮助用户发现对自己有价值的信息，另一方面让信息能够展现在对他感兴趣的人群中，从而实现信息提供商与用户的双赢。

tuijian.png

分类

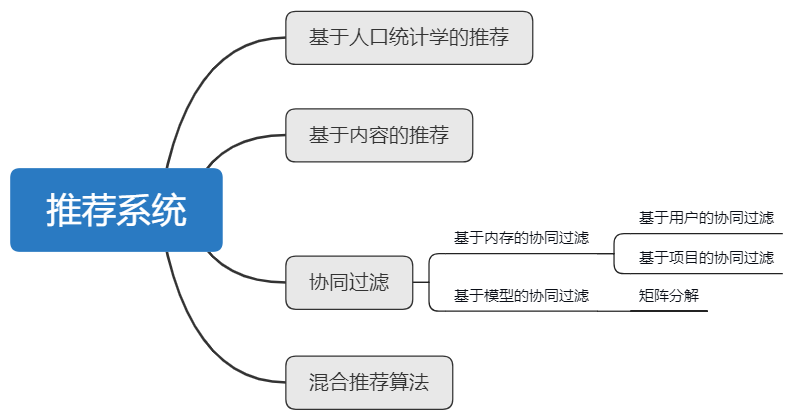
基于人口统计学的推荐

这是最为简单的一种推荐算法，系统首先会根据用户的属性建模，比如用户的年龄，性别，兴趣等信息。根据这些特征计算用户间的相似度。比如系统通过计算发现用户A和C比较相似。就会把A喜欢的物品推荐给C。

基于内容的推荐

与上面的方法相类似，只不过这次的中心转到了物品本身。使用物品本身的相似度而不是用户的相似度。

协同过滤

协同过滤又分为基于用户的协同过滤和基于物品的协同过滤,这些在后续的文章,我也会介绍。

混合推荐算法

以上介绍的方法是推荐领域最常见的几种方法。但是可以看出，每个方法都不是完美的。因此实际应用中，向Amazon这样的系统都是混合使用各种推荐算法，各取所长。因此我们在使用时，也可以多考虑一下什么情况下更适合使用哪种算法，来提高我们系统的效率。

在介绍完上面的分类之后你可能会发现我们今天所要学习到现在并未提到,但实际却是我们早就提及,只不过没有细化出来,下面我将开始说明介绍:

矩阵分解

介绍

通过上面介绍,我们已经知道了:推荐系统中最为主流与经典的技术之一是协同过滤技术（Collaborative Filtering），它是基于这样的假设：用户如果在过去对某些项目产生过兴趣，那么将来他很可能依然对其保持热忱。其中协同过滤技术又可根据是否采用了机器学习思想建模的不同划分为基于内存的协同过滤（Memory-based CF）与基于模型的协同过滤技术（Model-based CF）。其中基于内存的协同过滤又可以分为基于项目的协同过滤(ItemCF)和基于用户的协同过滤(UserCF),而在基于模型的协同过滤技术中尤为矩阵分解（Matrix Factorization,MF）技术最为普遍和流行，因为它的可扩展性极好并且易于实现，因此接下来我们将梳理下推荐系统中出现过的经典的矩阵分解方法。

tu.png

推导

我们知道，要做推荐系统，最基本的一个数据就是，用户-物品的评分矩阵:

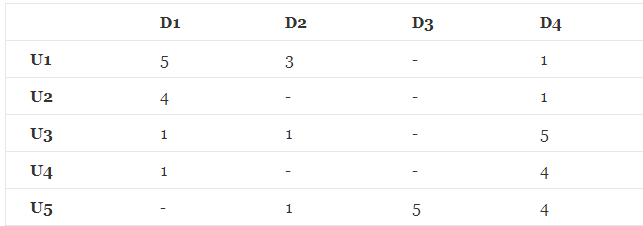
biao.png

矩阵中，描述了5个用户(U1,U2,U3,U4 ,U5)对4个物品(D1,D2,D3,D4)的评分(1-5分)，- 表示没有评分，现在目的是把没有评分的 给预测出来，然后按预测的分数高低，给用户进行推荐。

推导开始:

如何预测缺失的评分呢？对于缺失的评分，可以转化为基于机器学习的回归问题，也就是连续值的预测，对于矩阵分解有如下式子，R是类似上图的评分矩阵，假设N*M维(N表示行数，M表示列数)，可以分解为P跟Q矩阵，其中P矩阵维度N*K，P矩阵维度K*M。

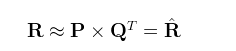1.png式子1

对于P,Q矩阵的解释，直观上，P矩阵是N个用户对K个主题的关系，Q矩阵是K个主题跟M个物品的关系，至于K个主题具体是什么，在算法里面K是一个参数，需要调节的，通常10~100之间。

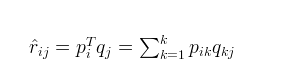2.png式子2

对于式子2的左边项，表示的是R^ 第i行，第j列的元素值，对于如何衡量，我们分解的好坏呢，式子3，给出了衡量标准，也就是损失函数，平方项损失，最后的目标，就是每一个元素(非缺失值)的e(i,j)的总和 最小

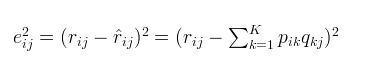3.png式子3

OK，目前现在评分矩阵有了，损失函数也有了，该优化算法登场了，下面式子4是基于梯度下降的优化算法，p,q里面的每个元素的更新方式

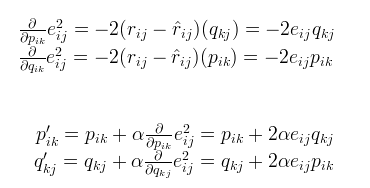4.png式子4

然而，机器学习算法都喜欢加一个正则项，这里面对式子3稍作修改，得到如下式子5，beita 是正则参数

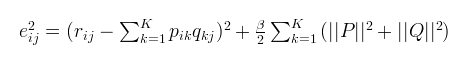5.png式子5

相应的p,q矩阵各个元素的更新也换成了如下方式

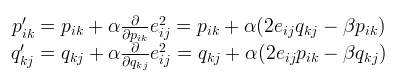6.png式子6
至此，P,Q矩阵元素求出来了之后，计算某个用户i对某个物品j的评分计算就是p(i,1)q(1,j)+p(i,2)q(2,j)+....+p(i,k)*q(k,j)。

算法步骤

1）随机生成两个矩阵P,Q；

2）为了能够有较好的泛化能力，会在损失函数中加入正则项对参数进行约束；

5.png

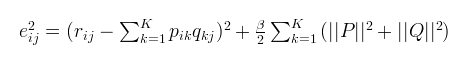
3）使用梯度下降法获得修正的p和q；

6.png

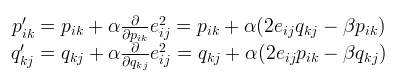
4）不停迭代直至算法最终收敛，即：直到sum（e^2）<=阈值或者达到指定的训练次数。

注意:算法步骤中的更新公式和损失函数都已经进行了正则化。

(★补充)正则化:

1）过拟合和欠拟合

一、欠拟合

训练误差和验证误差都很大，这种情况称为欠拟合。出现欠拟合的原因是模型尚未学习到数据的真实结构。因此，模拟在训练集和测试集上的性能都很差。

二、过拟合

模型在训练集上表现很好，但是在测试集上却不能保持准确，也就是模型泛化能力很差。这种情况很可能是模型过拟合。

区分训练集,测试集,验证集:

  • 训练集

作用：估计模型

学习样本数据集，通过匹配一些参数来建立一个分类器。建立一种分类的方式，主要是用来训练模型的。

  • 验证集

作用：确定网络结构或者控制模型复杂程度的参数

对学习出来的模型，调整分类器的参数，如在神经网络中选择隐藏单元数。验证集还用来确定网络结构或者控制模型复杂程度的参数。

  • 测试集

作用：检验最终选择最优的模型的性能如何

主要是测试训练好的模型的分辨能力（识别率等）

总结为:

在训练集上的效果 在测试集上的效果 具体情况
不好 不好 欠拟合
好 不好 过拟合
好 好 正常

2） 解决过拟合和欠拟合问题

一、解决欠拟合

(1)增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间;

(2)尝试非线性模型，比如核SVM 、决策树、DNN等模型;

(3)如果有正则项可以较小正则项参数 λ;

(4)增大数据集(最根本的方法);

(5)Boosting ,Boosting 往往会有较小的 Bias，比如 Gradient Boosting 等.

二、解决过拟合

(1)交叉检验，通过交叉检验得到较优的模型参数;

(2)特征选择，减少特征数或使用较少的特征组合，对于按区间离散化的特征，增大划分的区间;

(3)正则化，常用的有 L1、L2 正则。而且 L1正则还可以自动进行特征选择;

(4)如果有正则项则可以考虑增大正则项参数 λ;

(5)增加训练数据可以有限的避免过拟合;

(6)Bagging ,将多个弱学习器Bagging 一下效果会好很多，比如随机森林等;

(7)神经网络中解决过拟合可以采用dropout方法.

代码练习

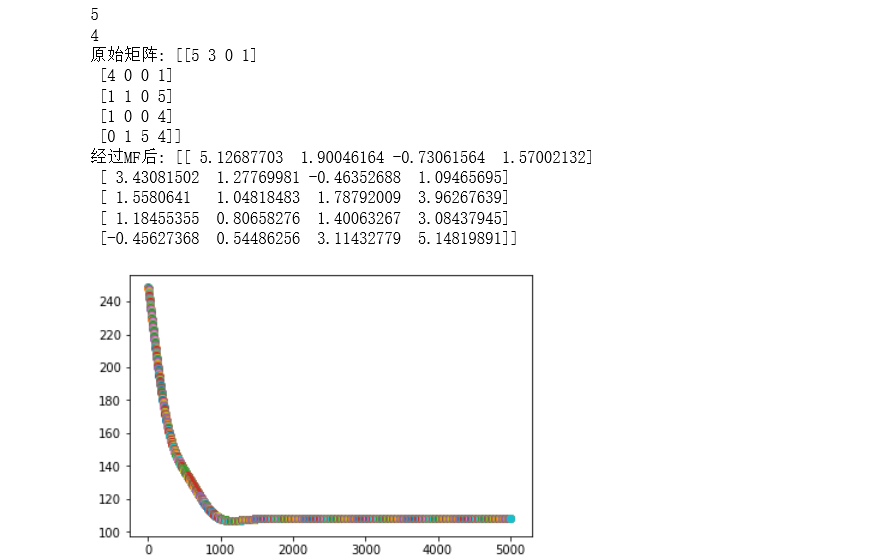
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import numpy as np
from math import pow
import matplotlib.pyplot as plt
%matplotlib inline

def mf(R,P,Q,K):
    alpha = 0.0002
    beta = 0.02
    times = 5000
    eplison = 0.001
    result = []
    #将矩阵Q进行转置
    Q = Q.T
    #将生成的矩阵相乘
    for time in range(times):
        #求R尖的值
        for i in range(len(R)):
            for j in range(len(R[i])):
                eij = R[i][j] - np.dot(P[i,:],Q[:,j])
                for k in range(K):
                    P[i][k] = P[i][k] + 2*alpha*eij*Q[k][j]
                    Q[k][j] = Q[k][j] + 2*alpha*eij*P[i][k]
        eR = np.dot(P,Q)
        #求eij的平方
        eij_2 = 0
        for i in range(len(R)):
            for j in range(len(R[i])):
                for k in range(K):
                    eij_2 = eij_2 + pow((R[i][j] - np.dot(P[i,:],Q[:,j])),2) + 0.5*beta*(pow(P[i][k],2))+pow(Q[k][j],2)
        result.append(eij_2)
        if eij_2 < eplison:
            break
    return P,Q.T,result 



def main():
    R = [
        [5,3,0,1],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,0,4],
        [0,1,5,4]
    ]
    #将R列表转化为矩阵
    R = np.array(R)
    #获取该矩阵的大小
    N = len(R)
    M = len(R[0])

    print(N)
    print(M)
    ''' 
    如何预测缺失的评分呢？对于缺失的评分，可以转化为基于机器学习的回归问题，也就是连续值的预测，
    对于矩阵分解有如下式子，R是类似图1的评分矩阵，假设N*M维(N表示行数，M表示列数)，可以分解为P跟Q矩阵，
    其中P矩阵维度N*K，P矩阵维度K*M。
    对于P,Q矩阵的解释，直观上，P矩阵是N个用户对K个主题的关系，Q矩阵是K个主题跟M个物品的关系，至于K个
    主题具体是什么，在算法里面K是一个参数，需要调节的，通常10~100之间。
    '''
    K = 2
    P = np.random.rand(N,K)
    Q = np.random.rand(M,K)
    #调用矩阵分解的函数
    mf_P,mf_Q,result = mf(R,P,Q,K)
    print("原始矩阵:",R)
    mf_R = np.dot(mf_P,mf_Q.T)
    print("经过MF后:",mf_R)
    #做出图像
    for t in range(5000):
        plt.scatter(t,result[t])
    plt.show()
main()
矩阵分解运行结果查看

mfjg.png

ip2.png