

K-均值算法概述¶

介绍¶

聚类与分类算法的最大区别在于, 分类的目标类别已知(监督学习), 而聚类的目标类别是未知的(无监督学习)。K-Means算法(K-均值算法)就是无监督算法之一，主要用于样本的聚类。其思想很简单，对于给定的样本集，按照样本与聚类中心之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连接在一起,让簇间的距离尽量的大。

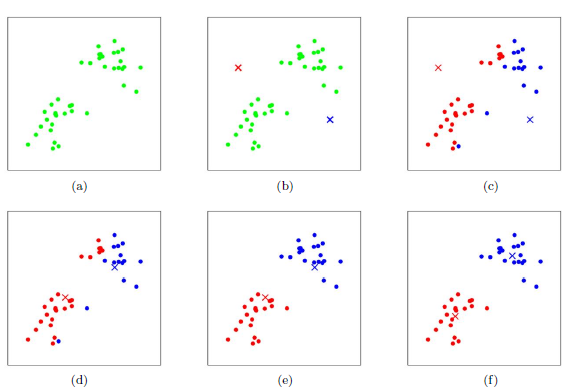
上图a表达了初始的数据集，假设k=2。在图b中，我们随机选择了两个k类所对应的类别质心，即图中的红色质心和蓝色质心，然后分别求样本中所有点到这两个质心的距离，并标记每个样本的类别为和该样本距离最小的质心的类别，如图c所示，经过计算样本和红色质心和蓝色质心的距离，我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心，如图4所示，新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程，即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。

当然在实际K-Mean算法中，我们一般会多次运行图c和图d，才能达到最终的比较优的类别。

算法步骤¶

步骤描述¶

1）数据准备:需要数值型数据类计算距离, 也可以将标称型数据映射为二值型数据再用于距离计算。

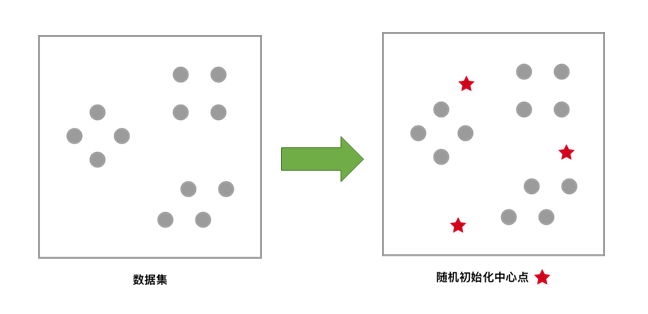
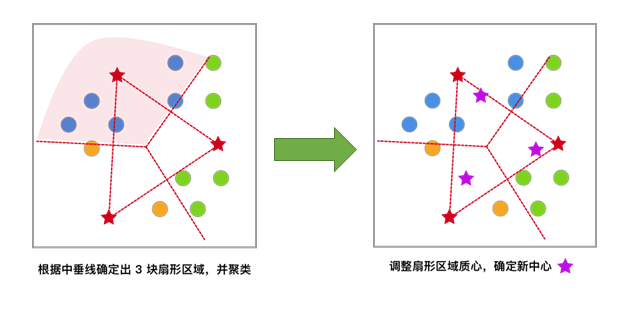
2）对于未聚类数据集，首先随机初始化 K 个（代表拟聚类簇个数）中心点，如图红色五角星所示。

3）每一个样本按照距离自身最近的中心点进行聚类(计算距离)，等效于通过两中心点连线的中垂线划分区域。

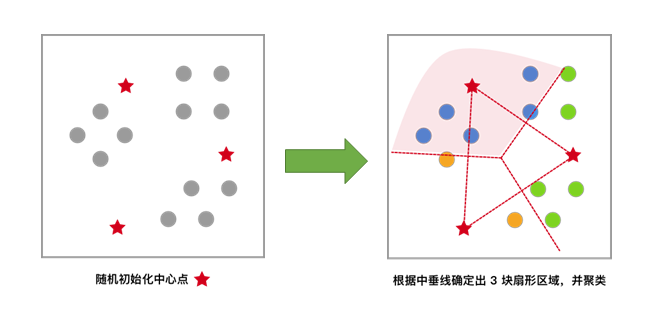
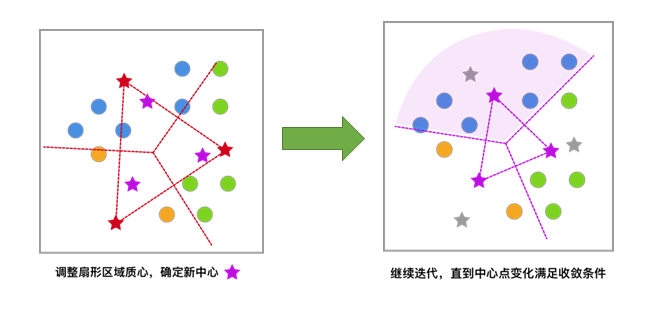
4）依据上次聚类结果，移动中心点到个簇的质心位置(新的质心的位置为新簇内点的x和y分别的的平均值)，并将此质心作为新的中心点。

5）反复迭代，直至中心点的变化满足收敛条件（变化很小或几乎不变化），最终得到聚类结果。

关于距离的计算¶

这里的距离指的是平面上两个点的直线距离。常用的距离计算公式有：

闵可夫斯基距离
欧几里得距离
曼哈顿距离
切比雪夫距离
马氏距离
余弦相似度
皮尔逊相关系数
汉明距离
杰卡德相似系数
编辑距离
DTW 距离
KL 散度

关于K值的选择¶

1）手肘法

在介绍之前我们先了解一个概念:SSE(sum of the squared errors，误差平方和)

手肘法的核心思想：

随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。
当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。

2）轮廓系数

使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值。

优缺点¶

优点:¶

属于无监督学习，无须准备训练集；
原理简单，实现起来较为容易；
结果可解释性较好。

缺点:¶

聚类数目k是一个输入参数。选择不恰当的k值可能会导致糟糕的聚类结果，这也是为什么要进行特征检查来决定数据集的聚类数目了；
可能收敛到局部最小值, 在大规模数据集上收敛较慢；
对于异常点、离群点敏感。

推导¶

下面给大家一个实例,供大家参考:

传统K-means改进¶

在学习了传统K-means算法的基础上,我们清楚了K-means的局限性,因此我们将要说一下K-Means的优化变体方法。这其中包括初始化优化K-Means++, 距离计算优化elkan K-Means算法和大数据情况下的优化Mini Batch K-Means算法。

K-means++¶

在学习K-means算法时我们提到，k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响，因此需要选择合适的k个质心。如果仅仅是完全随机的选择，有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化。

elkan K-means¶

在传统的K-Means算法中，我们在每轮迭代时，要计算所有的样本点到所有的质心的距离，这样会比较的耗时。那么，对于距离的计算有没有能够简化的地方呢？elkan K-Means算法就是从这块入手加以改进。它的目标是减少不必要的距离的计算。

Mini Batch K-means¶

在统的K-Means算法中，要计算所有的样本点到所有的质心的距离。如果样本量非常大，比如达到10万以上，特征有100以上，此时用传统的K-Means算法非常的耗时，就算加上elkan K-Means优化也依旧。在大数据时代，这样的场景越来越多。此时Mini Batch K-Means应运而生。

顾名思义，Mini Batch，也就是用样本集中的一部分的样本来做传统的K-Means，这样可以避免样本量太大时的计算难题，算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。

注意:此部分为扩展内容,如果你想真正的去优化你的算法,更详细的优化步骤你可以去刘建平Pinard-K-Means聚类算法原理或者是百度一下。

代码实现¶

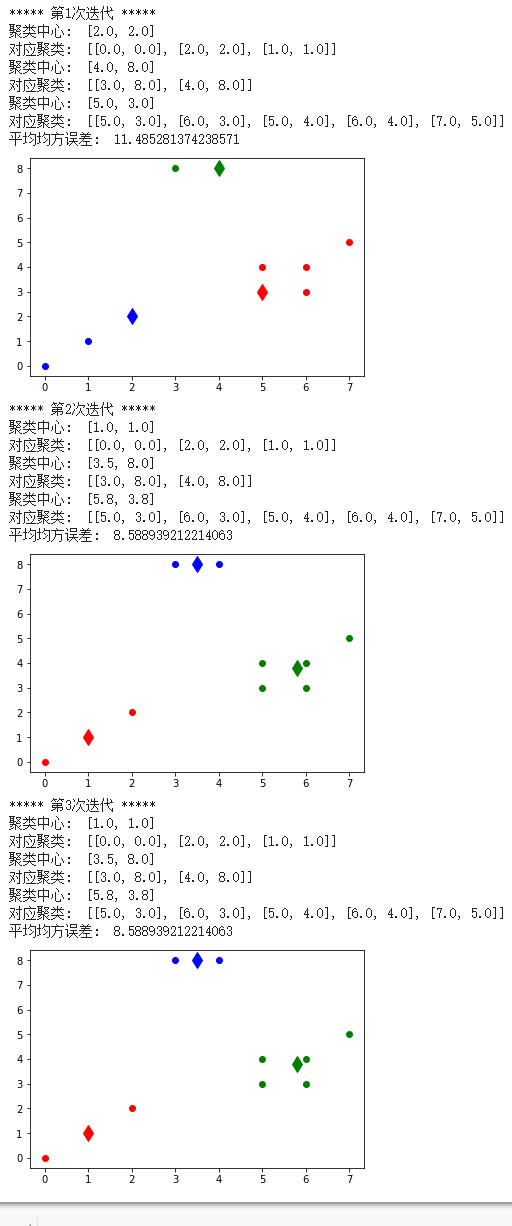
import numpy
import random
import matplotlib.pyplot as plt


def findCentroids(data_get, k):    # 随机获取k个质心
    return random.sample(data_get, k)


def calculateDistance(vecA, vecB):    # 计算向量vecA和向量vecB之间的欧氏距离
    return numpy.sqrt(numpy.sum(numpy.square(vecA - vecB)))


def minDistance(data_get, centroidList):
    # 计算data_get中的元素与centroidList中k个聚类中心的欧式距离，找出距离最小的
    # 将该元素加入相应的聚类中
    clusterDict = dict()  # 用字典存储聚类结果
    for element in data_get:
        vecA = numpy.array(element)  # 转换成数组形式
        flag = 0  # 元素分类标记，记录与相应聚类距离最近的那个类
        minDis = float("inf")  # 初始化为最大值

        for i in range(len(centroidList)):
            vecB = numpy.array(centroidList[i])
            distance = calculateDistance(vecA, vecB)  # 两向量间的欧式距离
            if distance < minDis:
                minDis = distance
                flag = i  # 保存与当前item距离最近的那个聚类的标记

        if flag not in clusterDict.keys():  # 簇标记不存在，进行初始化
            clusterDict[flag] = list()
        clusterDict[flag].append(element)  # 加入相应的类中

    return clusterDict  # 返回新的聚类结果


def getCentroids(clusterDict):
    centroidList = list()
    for key in clusterDict.keys():
        centroid = numpy.mean(numpy.array(clusterDict[key]), axis=0)  # 求聚类中心即求解每列的均值
        centroidList.append(centroid)

    return numpy.array(centroidList).tolist()


def calculate_Var(clusterDict, centroidList):
    # 计算聚类间的均方误差
    # 将类中各个向量与聚类中心的距离进行累加求和

    sum = 0.0
    for key in clusterDict.keys():
        vecA = numpy.array(centroidList[key])
        distance = 0.0
        for item in clusterDict[key]:
            vecB = numpy.array(item)
            distance += calculateDistance(vecA, vecB)
        sum += distance
    return sum


def showCluster(centroidList, clusterDict):
    # 画聚类结果
    colorMark = ['or', 'ob', 'og', 'ok', 'oy', 'ow']  # 元素标记
    centroidMark = ['dr', 'db', 'dg', 'dk', 'dy', 'dw']  # 聚类中心标记
    for key in clusterDict.keys():
        plt.plot(centroidList[key][0], centroidList[key][1], centroidMark[key], markersize=12)  # 画聚类中心
        for item in clusterDict[key]:
            plt.plot(item[0], item[1], colorMark[key])  # 画类下的点
    plt.show()


data = [[0.0, 0.0], [3.0, 8.0], [2.0, 2.0], [1.0, 1.0], [5.0, 3.0],
        [4.0, 8.0], [6.0, 3.0], [5.0, 4.0], [6.0, 4.0], [7.0, 5.0]]


if __name__ == '__main__':

    centroidList = findCentroids(data, 3)  # 随机获取3个聚类中心
    clusterDict = minDistance(data, centroidList)  # 第一次聚类迭代
    newVar = calculate_Var(clusterDict, centroidList)  # 计算均方误差值，通过新旧均方误差来获得迭代终止条件
    oldVar = -0.0001  # 初始化均方误差

    print('***** 第1次迭代 *****')
    for key in clusterDict.keys():
        print('聚类中心: ', centroidList[key])
        print('对应聚类: ',clusterDict[key])
    print('平均均方误差: ', newVar)
    showCluster(centroidList, clusterDict)  # 展示聚类结果

    k = 2
    while abs(newVar - oldVar) >= 0.0001:  # 当连续两次聚类结果差距小于0.0001时，迭代结束
        centroidList = getCentroids(clusterDict)  # 获得新的聚类中心
        clusterDict = minDistance(data, centroidList)  # 新的聚类结果
        oldVar = newVar
        newVar = calculate_Var(clusterDict, centroidList)

        print('***** 第%d次迭代 *****' % k)

        for key in clusterDict.keys():
            print('聚类中心: ', centroidList[key])
            print('对应聚类: ', clusterDict[key])
        print('平均均方误差: ', newVar)
        showCluster(centroidList, clusterDict)  # 展示聚类结果
        k += 1

K-means运行结果查看