跳转至

卷积神经网络概述

在前面的文章中，我们介绍了全连接神经网络，然而这种结构的网络对于图像识别任务来说并不是很合适。本文将要介绍一种更适合图像、语音识别任务的神经网络结构——卷积神经网络(Convolutional Neural Network, CNN)。说卷积神经网络是最重要的一种神经网络也不为过，它在最近几年大放异彩，几乎所有图像、语音识别领域的重要突破都是卷积神经网络取得的，比如谷歌的GoogleNet、微软的ResNet等，打败李世石的AlphaGo也用到了这种网络。本文将详细介绍卷积神经网络。

介绍

全连接神经网络 VS 卷积网络

全连接神经网络之所以不太适合图像识别任务，主要有以下几个方面的问题：

  1. 参数数量太多 考虑一个输入1000*1000像素的图片(一百万像素，现在已经不能算大图了)，输入层有1000*1000=100万节点。假设第一个隐藏层有100个节点(这个数量并不多)，那么仅这一层就有(1000*1000+1)*100=1亿参数，这实在是太多了！我们看到图像只扩大一点，参数数量就会多很多，因此它的扩展性很差。

  2. 没有利用像素之间的位置信息 对于图像识别任务来说，每个像素和其周围像素的联系是比较紧密的，和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连，那么就相当于对于一个像素来说，把图像的所有像素都等同看待，这不符合前面的假设。当我们完成每个连接权重的学习之后，最终可能会发现，有大量的权重，它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重，这样的学习必将是非常低效的。

  3. 网络层数限制 我们知道网络层数越多其表达能力越强，但是通过梯度下降方法训练深度全连接神经网络很困难，因为全连接神经网络的梯度很难传递超过3层。因此，我们不可能得到一个很深的全连接神经网络，也就限制了它的能力。

那么，卷积神经网络又是怎样解决这个问题的呢？主要有三个思路：

  1. 局部连接 这个是最容易想到的，每个神经元不再和上一层的所有神经元相连，而只和一小部分神经元相连。这样就减少了很多参数。

  2. 权值共享 一组连接可以共享同一个权重，而不是每个连接有一个不同的权重，这样又减少了很多参数。

  3. 下采样 可以使用Pooling来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。

对于图像识别任务来说，卷积神经网络通过尽可能保留重要的参数，去掉大量不重要的参数，来达到更好的学习效果。

接下来，我们将详述卷积神经网络到底是何方神圣。

认识

首先，我们先获取一个感性认识，下图是一个卷积神经网络的示意图：

t.png
网络架构

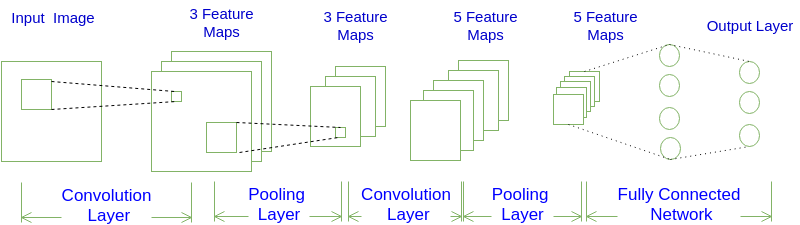
如图所示，一个卷积神经网络由若干卷积层、Pooling层、全连接层组成。你可以构建各种不同的卷积神经网络，它的常用架构模式为：

INPUT -> [[CONV]N -> POOL?]M -> [FC]*K

也就是N个卷积层叠加，然后(可选)叠加一个Pooling层，重复这个结构M次，最后叠加K个全连接层。

对于上图展示的卷积神经网络：

INPUT -> CONV -> POOL -> CONV -> POOL -> FC -> FC

按照上述模式可以表示为：

INPUT -> [[CONV]1 -> POOL]2 -> [FC]*2

也就是：N=1, M=2, K=2。

结构

从上图我们可以发现卷积神经网络的层结构和全连接神经网络的层结构有很大不同。全连接神经网络每层的神经元是按照一维排列的，也就是排成一条线的样子；而卷积神经网络每层的神经元是按照三维排列的，也就是排成一个长方体的样子，有宽度、高度和深度。

对于上图展示的神经网络，我们看到输入层的宽度和高度对应于输入图像的宽度和高度，而它的深度为1。接着，第一个卷积层对这幅图像进行了卷积操作(后面我们会讲如何计算卷积)，得到了三个Feature Map。这里的"3"可能是让很多初学者迷惑的地方，实际上，就是这个卷积层包含三个Filter，也就是三套参数，每个Filter都可以把原始输入图像卷积得到一个Feature Map，三个Filter就可以得到三个Feature Map。至于一个卷积层可以有多少个Filter，那是可以自由设定的。也就是说，卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征，三个Filter就对原始图像提取出三组不同的特征，也就是得到了三个Feature Map，也称做三个通道(channel)。

继续观察上图，在第一个卷积层之后，Pooling层对三个Feature Map做了下采样(后面我们会讲如何计算下采样)，得到了三个更小的Feature Map。接着，是第二个卷积层，它有5个Filter。每个Fitler都把前面下采样之后的3个Feature Map卷积在一起，得到一个新的Feature Map。这样，5个Filter就得到了5个Feature Map。接着，是第二个Pooling，继续对5个Feature Map进行下采样，得到了5个更小的Feature Map。

上图所示网络的最后两层是全连接层。第一个全连接层的每个神经元，和上一层5个Feature Map中的每个神经元相连，第二个全连接层(也就是输出层)的每个神经元，则和第一个全连接层的每个神经元相连，这样得到了整个网络的输出。

至此，我们对卷积神经网络有了最基本的感性认识。接下来，我们将介绍卷积神经网络中各种层的计算。

计算

卷积(Convolution)层输出值计算

我们用一个简单的例子来讲述如何计算卷积，然后，我们抽象出卷积层的一些重要概念和计算方法。

假设有一个55的图像，使用一个33的filter进行卷积，想得到一个3*3的Feature Map，如下所示：

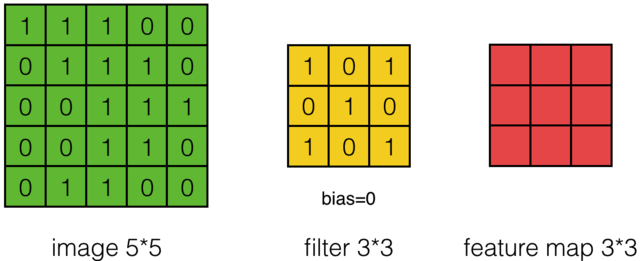
pc1.png

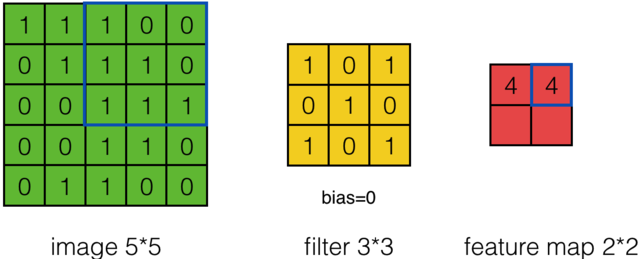
为了清楚的描述卷积计算过程，我们首先对图像的每个像素进行编号，用Xi,j表示图像的第i行第j列元素；对filter的每个权重进行编号，用Wm,n表示第m行第n列权重，用Wb表示filter的偏置项；对Feature Map的每个元素进行编号，用ai,j表示Feature Map的第i行第j列元素；用f表示激活函数(这个例子选择relu函数作为激活函数)。然后，使用下列公式计算卷积：

pc2.png

计算结果如下图所示：

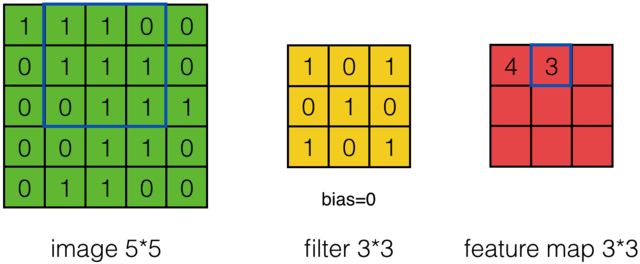
pc3.png

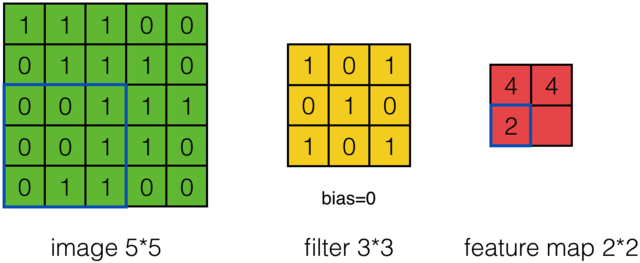
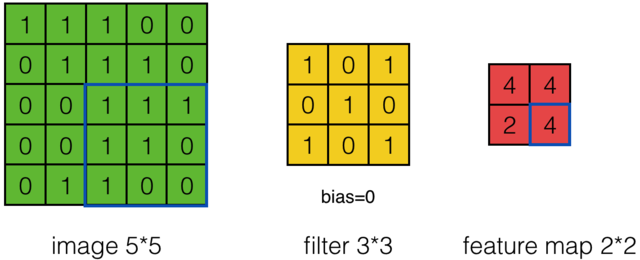
可以依次计算出Feature Map中所有元素的值。下面的动画显示了整个Feature Map的计算过程：

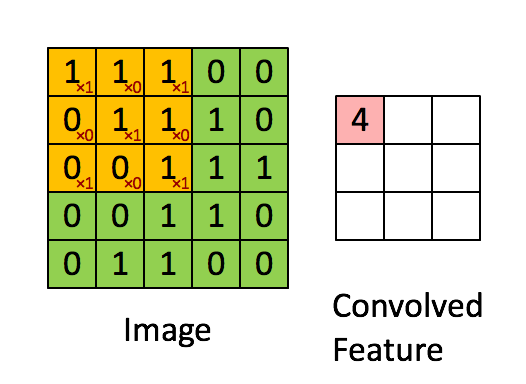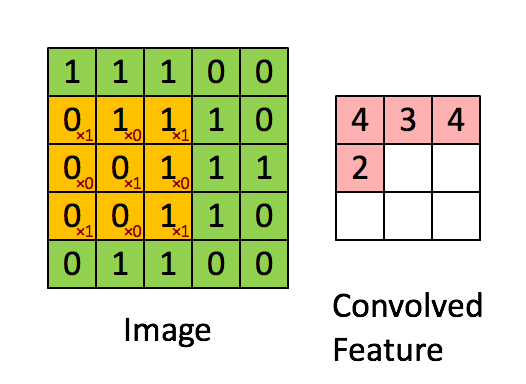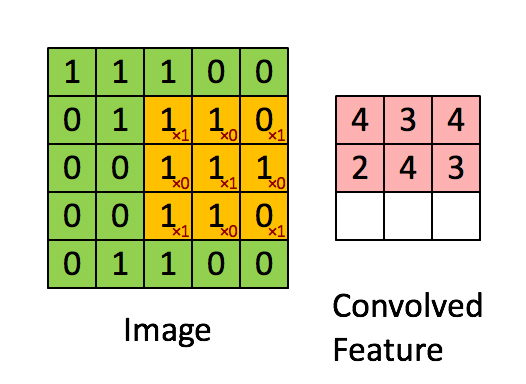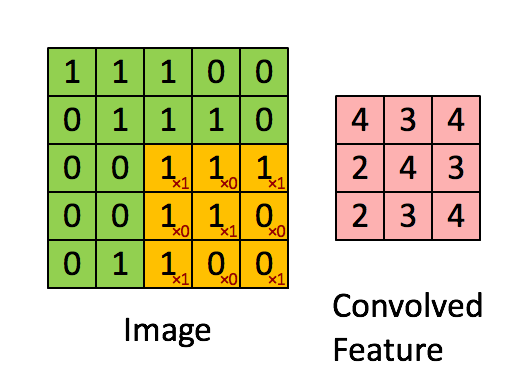
pcc.gif

上面的计算过程中，步幅(stride)为1。步幅可以设为大于1的数。例如，当步幅为2时，Feature Map计算如下：

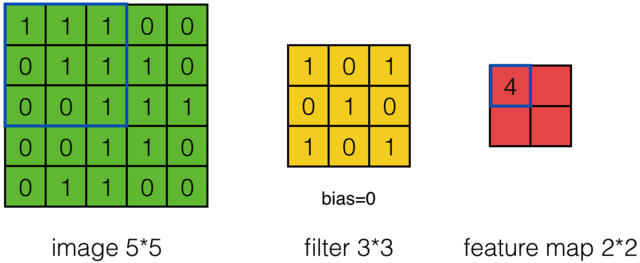
pc4.png
pc5.png
pc6.png
pc7.png
我们注意到，当步幅设置为2的时候，Feature Map就变成2*2了。这说明图像大小、步幅和卷积后的Feature Map大小是有关系的。事实上，它们满足下面的关系：
gs.png

前面我们已经讲了深度为1的卷积层的计算方法，如果深度大于1怎么计算呢？其实也是类似的。如果卷积前的图像深度为D，那么相应的filter的深度也必须为D。我们扩展一下式1，得到了深度大于1的卷积计算公式：

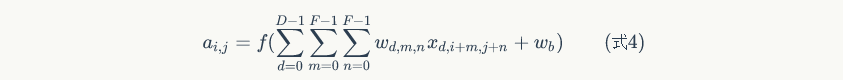
gs1.png

在式4中，D是深度；F是filter的大小(宽度或高度，两者相同)；表示filter的第层第行第列权重；Wd,m,n表示图像的第d层第m行第n列像素；其它的符号含义和式1是相同的，不再赘述。

我们前面还曾提到，每个卷积层可以有多个filter。每个filter和原始图像进行卷积后，都可以得到一个Feature Map。因此，卷积后Feature Map的深度(个数)和卷积层的filter个数是相同的。

下面的动画显示了包含两个filter的卷积层的计算。我们可以看到7*7*3输入，经过两个3*3*3filter的卷积(步幅为2)，得到了3*3*2的输出。另外我们也会看到下图的Zero padding是1，也就是在输入元素的周围补了一圈0。Zero padding对于图像边缘部分的特征提取是很有帮助的。

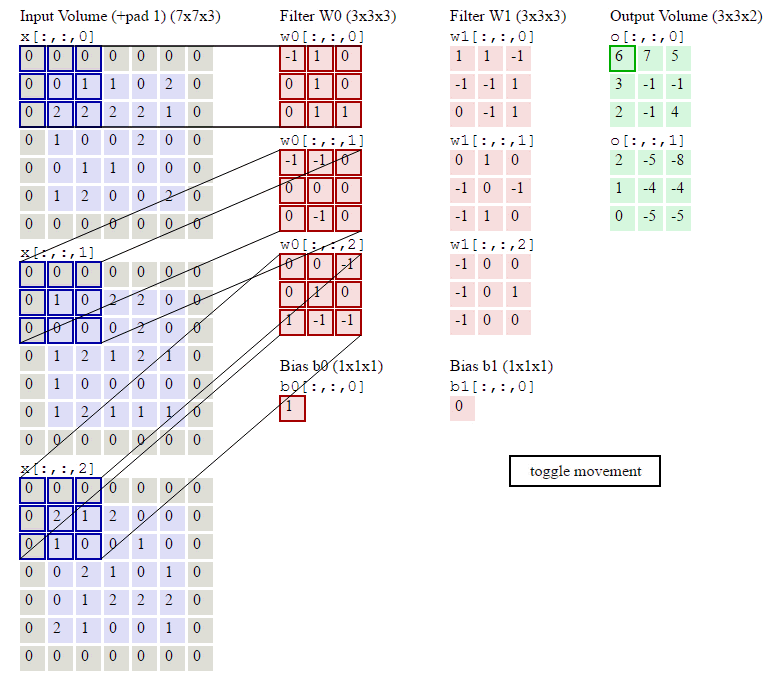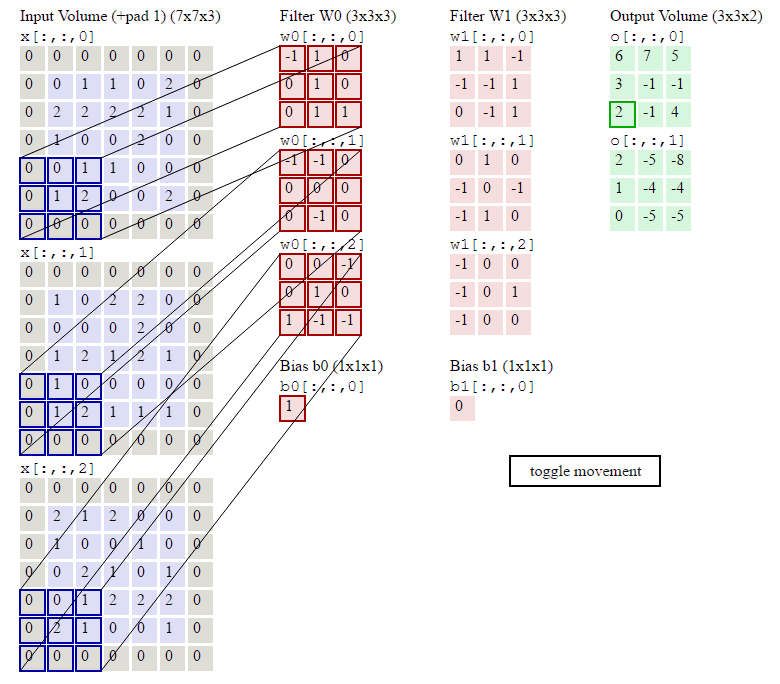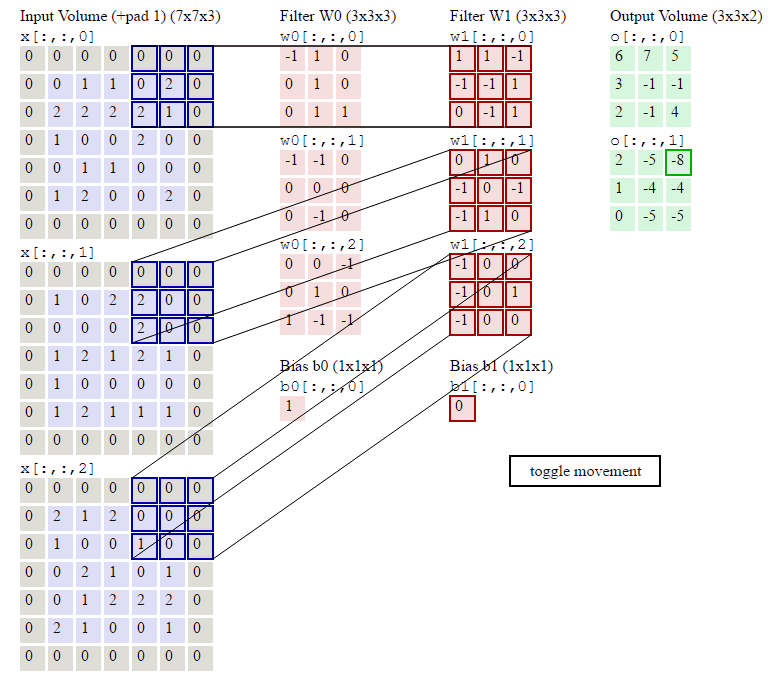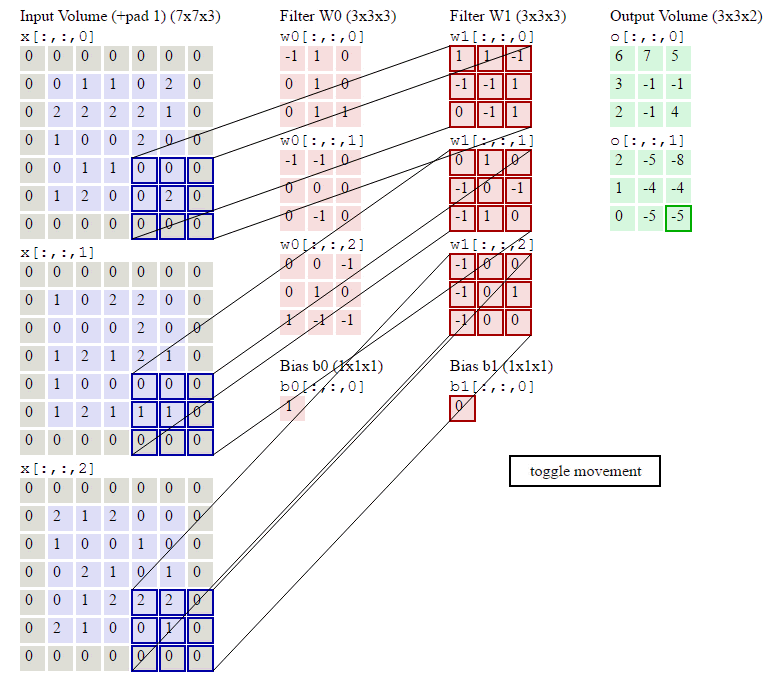
cc.gif

以上就是卷积层的计算方法。这里面体现了局部连接和权值共享：每层神经元只和上一层部分神经元相连(卷积计算规则)，且filter的权值对于上一层所有神经元都是一样的。对于包含两个3*3*3的fitler的卷积层来说，其参数数量仅有(3*3*3+1)*2=56个，且参数数量与上一层神经元个数无关。与全连接神经网络相比，其参数数量大大减少了。

式4的表达很是繁冗，最好能简化一下。就像利用矩阵可以简化表达全连接神经网络的计算一样，我们可以利用卷积公式来简化卷积神经网络的表达。

池化(Pooling)层输出值计算

Pooling层主要的作用是下采样，通过去掉Feature Map中不重要的样本，进一步减少参数数量。Pooling的方法很多，最常用的是Max Pooling。Max Pooling实际上就是在n*n的样本中取最大值，作为采样后的样本值。下图是2*2 max pooling：

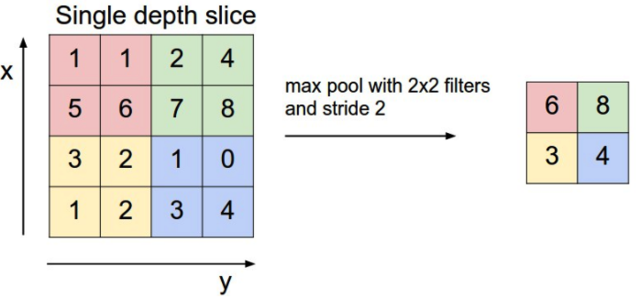
pool.png
除了Max Pooing之外，常用的还有Mean Pooling——取各样本的平均值。

对于深度为D的Feature Map，各层独立做Pooling，因此Pooling后的深度仍然为D。

全连接(Connected)层输出值计算

全连接层输出值的计算和上一篇文章神经网络讲过的全连接神经网络是一样的，这里就不再赘述了。

训练

和全连接神经网络相比，卷积神经网络的训练要复杂一些。但训练的原理是一样的：利用链式求导计算损失函数对每个权重的偏导数（梯度），然后根据梯度下降公式更新权重。训练算法依然是反向传播算法。

我们先回忆一下上一篇文章神经网络介绍的反向传播算法，整个算法分为三个步骤：

ggggss.png
对于卷积神经网络，由于涉及到局部连接、下采样的等操作，影响到了第二步误差项δ的具体计算方法，而权值共享影响了第三步权重的梯度的计算方法。接下来，我们分别介绍卷积层和Pooling层的训练算法。

卷积层训练

对于卷积层，我们先来看看上面的第二步，即如何将误差项δ传递到上一层；然后再来看看第三步，即如何计算filter每个权值的梯度。

卷积层误差项的传递

最简单情况下误差项的传递

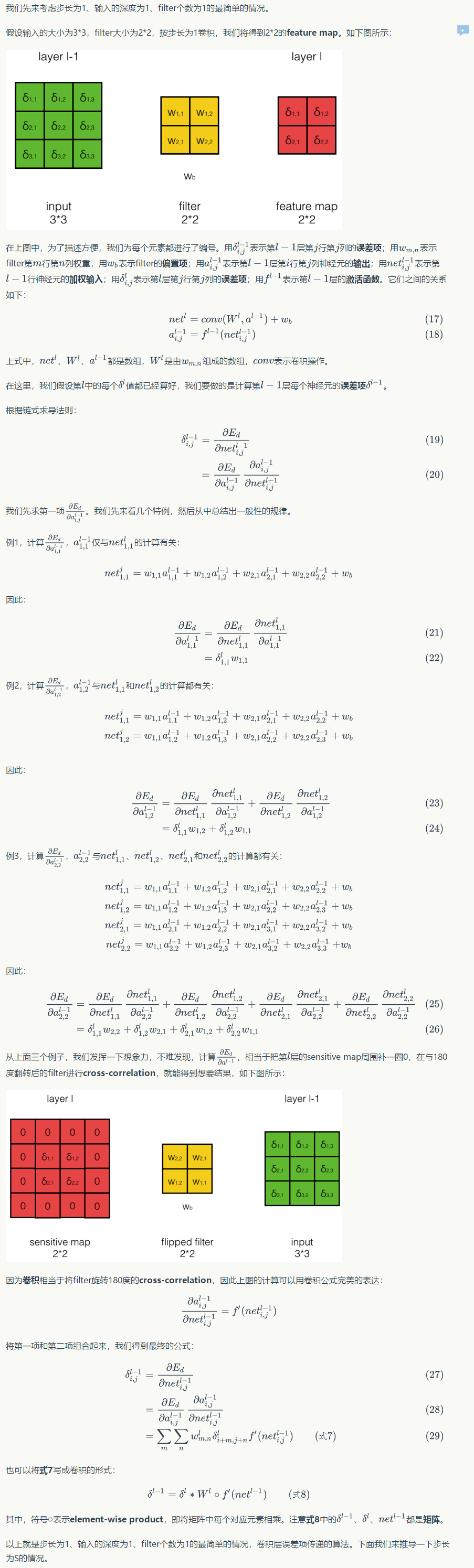
xin1.png

卷积步长为S时的误差传递

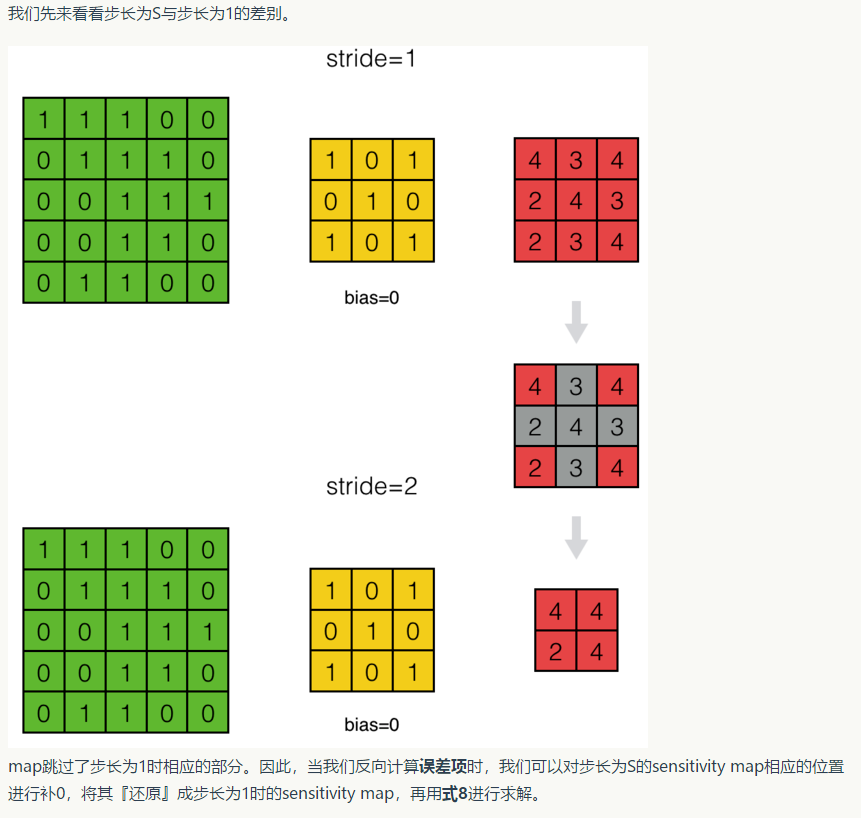
xin2.png

输入层深度为D时的误差传递

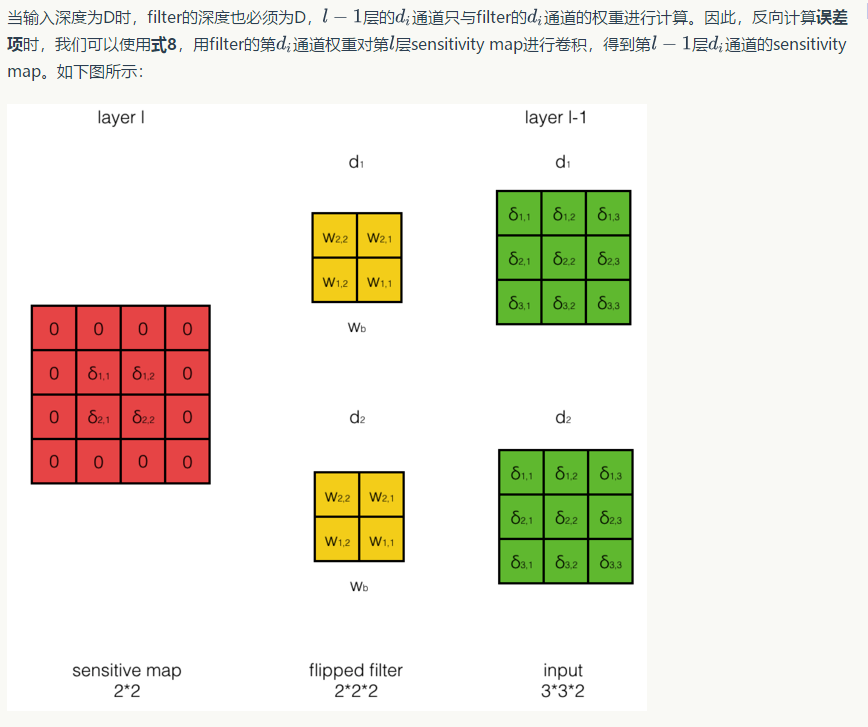
xin3.png

filter数量为N时的误差传递

xin4.png

卷积层filter权重梯度的计算

xin5.png

池化层训练

Max Pooling误差项的传递

xin6.png

Mean Pooling误差项的传递

xin7.png

经典的卷积神经网络

  1. LeNet

LeNet诞生于1994年，由深度学习三巨头之一的Yan LeCun提出，他也被称为卷积神经网络之父。LeNet主要用来进行手写字符的识别与分类，准确率达到了98%，并在美国的银行中投入了使用，被用于读取北美约10%的支票。LeNet奠定了现代卷积神经网络的基础。

  1. AlexNet

AlexNet由Hinton的学生Alex Krizhevsky于2012年提出，并在当年取得了Imagenet比赛冠军。AlexNet可以算是LeNet的一种更深更宽的版本，证明了卷积神经网络在复杂模型下的有效性，算是神经网络在低谷期的第一次发声，确立了深度学习，或者说卷积神经网络在计算机视觉中的统治地位。

  1. VGGNet

VGGNet是牛津大学计算机视觉组和Google DeepMind公司一起研发的深度卷积神经网络，并取得了2014年Imagenet比赛定位项目第一名和分类项目第二名。该网络主要是泛化性能很好，容易迁移到其他的图像识别项目上，可以下载VGGNet训练好的参数进行很好的初始化权重操作，很多卷积神经网络都是以该网络为基础，比如FCN，UNet，SegNet等。vgg版本很多，常用的是VGG16，VGG19网络。

  1. ResNet

ResNet（残差神经网络）由微软研究院的何凯明等4名华人于2015年提出，成功训练了152层超级深的卷积神经网络，效果非常突出，而且容易结合到其他网络结构中。在五个主要任务轨迹中都获得了第一名的成绩：

1
2
3
4
5
6
7
8
9
            ImageNet分类任务：错误率3.57%

            ImageNet检测任务：超过第二名16%

            ImageNet定位任务：超过第二名27%

            COCO检测任务：超过第二名11%

            COCO分割任务：超过第二名12%

发展图:

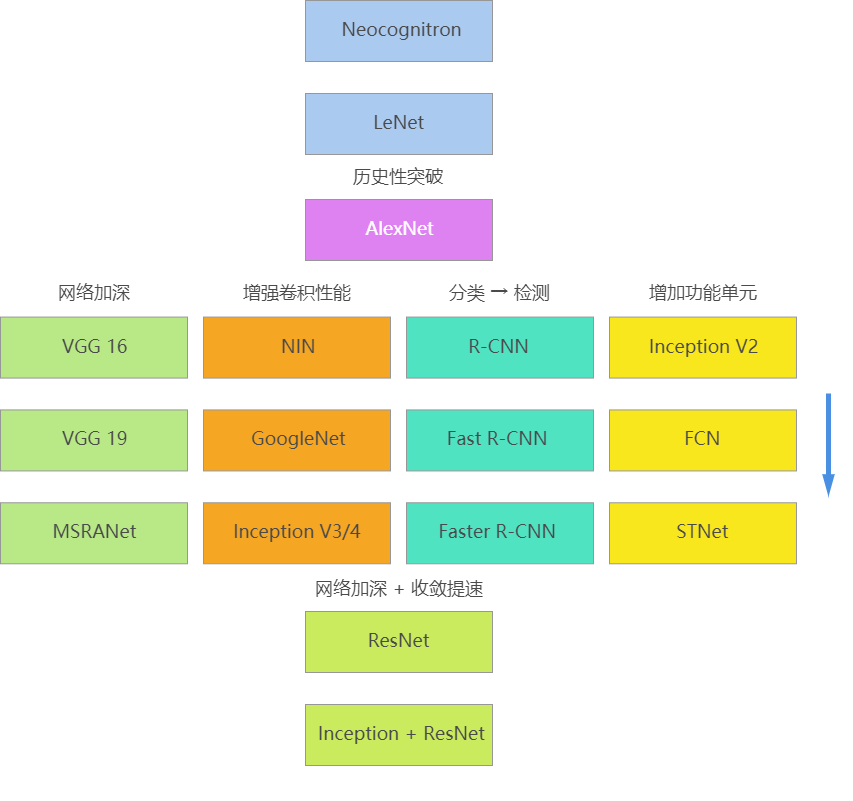
tz.png

代码实现

基于Tensorflow的CNN实现手写体识别

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#coding:utf-8
import tensorflow as tf
#import MNIST_data.input_data as input_data
from tensorflow.examples.tutorials.mnist import input_data
import time

"""
权重初始化
初始化为一个接近0的很小的正数
"""
def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev = 0.1)
    return tf.Variable(initial)

def bias_variable(shape):
    initial = tf.constant(0.1, shape = shape)
    return tf.Variable(initial)

"""
卷积和池化，使用卷积步长为1（stride size）,0边距（padding size）
池化用简单传统的2x2大小的模板做max pooling
"""
def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding = 'SAME')
    # tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)
    # x(input)  : [batch, in_height, in_width, in_channels]
    # W(filter) : [filter_height, filter_width, in_channels, out_channels]
    # strides   : The stride of the sliding window for each dimension of input.
    #             For the most common case of the same horizontal and vertices strides, strides = [1, stride, stride, 1]

def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize = [1, 2, 2, 1],
                          strides = [1, 2, 2, 1], padding = 'SAME')
    # tf.nn.max_pool(value, ksize, strides, padding, data_format='NHWC', name=None)
    # x(value)              : [batch, height, width, channels]
    # ksize(pool大小)        : A list of ints that has length >= 4. The size of the window for each dimension of the input tensor.
    # strides(pool滑动大小)   : A list of ints that has length >= 4. The stride of the sliding window for each dimension of the input tensor.

start = time.clock() #计算开始时间
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True) #MNIST数据输入

"""
第一层 卷积层

x_image(batch, 28, 28, 1) -> h_pool1(batch, 14, 14, 32)
"""
x = tf.placeholder(tf.float32,[None, 784])
x_image = tf.reshape(x, [-1, 28, 28, 1]) #最后一维代表通道数目，如果是rgb则为3 
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])

h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
# x_image -> [batch, in_height, in_width, in_channels]
#            [batch, 28, 28, 1]
# W_conv1 -> [filter_height, filter_width, in_channels, out_channels]
#            [5, 5, 1, 32]
# output  -> [batch, out_height, out_width, out_channels]
#            [batch, 28, 28, 32]
h_pool1 = max_pool_2x2(h_conv1)
# h_conv1 -> [batch, in_height, in_weight, in_channels]
#            [batch, 28, 28, 32]
# output  -> [batch, out_height, out_weight, out_channels]
#            [batch, 14, 14, 32]

"""
第二层 卷积层

h_pool1(batch, 14, 14, 32) -> h_pool2(batch, 7, 7, 64)
"""
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])

h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
# h_pool1 -> [batch, 14, 14, 32]
# W_conv2 -> [5, 5, 32, 64]
# output  -> [batch, 14, 14, 64]
h_pool2 = max_pool_2x2(h_conv2)
# h_conv2 -> [batch, 14, 14, 64]
# output  -> [batch, 7, 7, 64]

"""
第三层 全连接层

h_pool2(batch, 7, 7, 64) -> h_fc1(1, 1024)
"""
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])

h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

"""
Dropout

h_fc1 -> h_fc1_drop, 训练中启用，测试中关闭
"""
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

"""
第四层 Softmax输出层
"""
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])

y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

"""
训练和评估模型

ADAM优化器来做梯度最速下降,feed_dict中加入参数keep_prob控制dropout比例
"""
y_ = tf.placeholder("float", [None, 10])
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv)) #计算交叉熵
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) #使用adam优化器来以0.0001的学习率来进行微调
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1)) #判断预测标签和实际标签是否匹配
accuracy = tf.reduce_mean(tf.cast(correct_prediction,"float"))

sess = tf.Session() #启动创建的模型
sess.run(tf.initialize_all_variables()) #旧版本
#sess.run(tf.global_variables_initializer()) #初始化变量

for i in range(1000): #开始训练模型，循环训练5000次
    batch = mnist.train.next_batch(50) #batch大小设置为50
    if i % 100 == 0:
        train_accuracy = accuracy.eval(session = sess,
                                       feed_dict = {x:batch[0], y_:batch[1], keep_prob:1.0})
        print("step %d, train_accuracy %g" %(i, train_accuracy))
    train_step.run(session = sess, feed_dict = {x:batch[0], y_:batch[1],
                   keep_prob:0.5}) #神经元输出保持不变的概率 keep_prob 为0.5

print("test accuracy %g" %accuracy.eval(session = sess,
      feed_dict = {x:mnist.test.images, y_:mnist.test.labels,
                   keep_prob:1.0})) #神经元输出保持不变的概率 keep_prob 为 1，即不变，一直保持输出

end = time.clock() #计算程序结束时间
print("running time is:",(end-start))
卷积神经网络运行结果查看

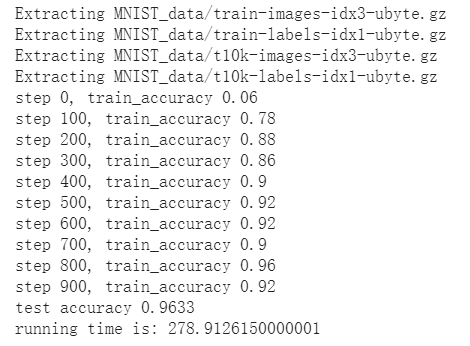
jjjg.png

其他实现

(后续更新...)

ip2.png

🎁文章末尾小彩蛋:一份深度学习的资料

①蓝奏云下载

②百度网盘备用下载(提取码:41j3)