贝叶斯个性化排序概述¶
排序推荐算法背景¶
排序推荐算法历史很悠久,早在做信息检索的各种产品中就已经在使用了。最早的第一类排序算法类别是点对方法(Pointwise Approach),这类算法将排序问题被转化为分类、回归之类的问题,并使用现有分类、回归等方法进行实现。第二类排序算法是成对方法(Pairwise Approach),在序列方法中,排序被转化为对序列分类或对序列回归。所谓的pair就是成对的排序,比如(a,b)一组表明a比b排的靠前。我们要讲到的BPR就属于这一类。第三类排序算法是列表方法(Listwise Approach),它采用更加直接的方法对排序问题进行了处理。它在学习和预测过程中都将排序列表作为一个样本。排序的组结构被保持。
BPR¶
使用背景¶
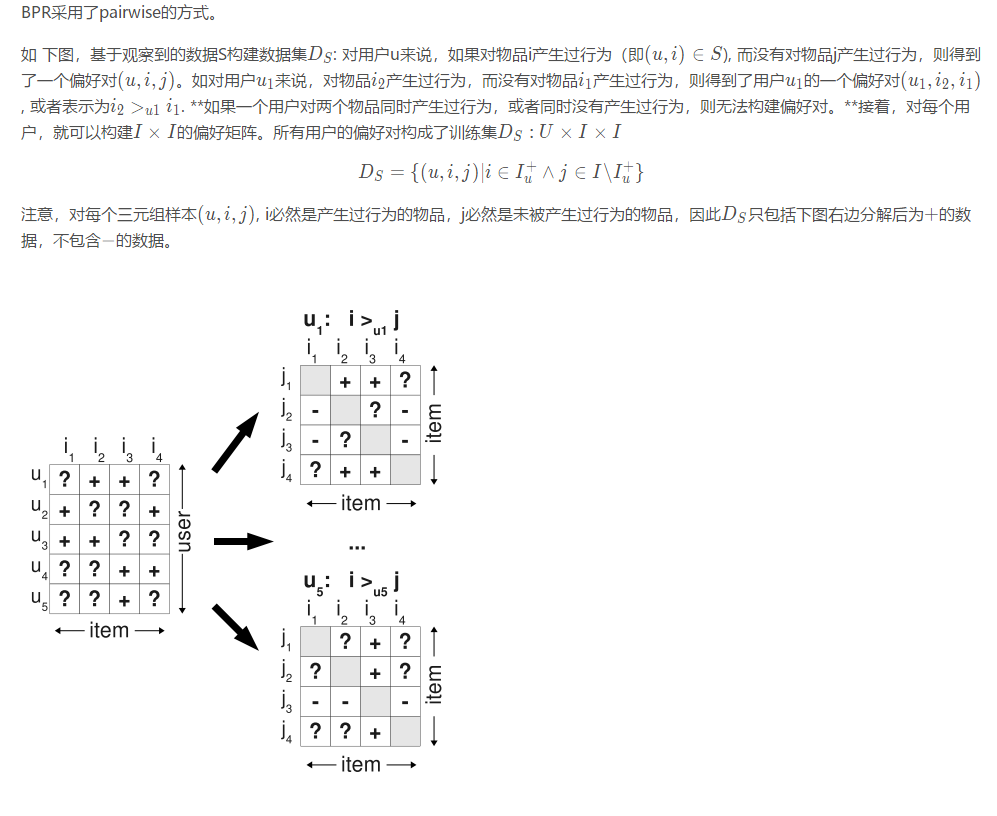
在很多推荐场景中,我们都是基于现有的用户和商品之间的一些数据,得到用户对所有商品的评分,选择高分的商品推荐给用户,这是funkSVD之类算法的做法,使用起来也很有效。但是在有些推荐场景中,我们是为了在千万级别的商品中推荐个位数的商品给用户,此时,我们更关心的是用户来说,哪些极少数商品在用户心中有更高的优先级,也就是排序更靠前。也就是说,我们需要一个排序算法,这个算法可以把每个用户对应的所有商品按喜好排序。BPR就是这样的一个我们需要的排序算法。
介绍¶
BPR即Bayesian Personalized Ranking,中文名称为贝叶斯个性化排序,是当下推荐系统中常用的一种推荐算法。与其他的基于用户评分矩阵的方法不同的是BPR主要采用用户的隐式反馈(如点击、收藏等),通过对问题进行贝叶斯分析得到的最大后验概率来对item进行排序,进而产生推荐。
定义¶

传统解决方式¶

BPR的解决方式¶

基于矩阵分解的BPR¶

一份更加专业的BPR学习资料在:刘建平-贝叶斯个性化排序(BPR)
代码实现¶
注意:
1)数据集+程序下载 。
2)程序每次运行结果不同,但上下偏差不大。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 | import random from collections import defaultdict import numpy as np from sklearn.metrics import roc_auc_score import scores class BPR: #用户数 user_count = 943 #项目数 item_count = 1682 #k个主题,k数 latent_factors = 20 #步长α lr = 0.01 #参数λ reg = 0.01 #训练次数 train_count = 1000 #训练集 train_data_path = 'train.txt' #测试集 test_data_path = 'test.txt' #U-I的大小 size_u_i = user_count * item_count # 随机设定的U,V矩阵(即公式中的Wuk和Hik)矩阵 U = np.random.rand(user_count, latent_factors) * 0.01 #大小无所谓 V = np.random.rand(item_count, latent_factors) * 0.01 biasV = np.random.rand(item_count) * 0.01 #生成一个用户数*项目数大小的全0矩阵 test_data = np.zeros((user_count, item_count)) #生成一个一维的全0矩阵 test = np.zeros(size_u_i) #再生成一个一维的全0矩阵 predict_ = np.zeros(size_u_i) #获取U-I数据对应 def load_data(self, path): user_ratings = defaultdict(set) with open(path, 'r') as f: for line in f.readlines(): u, i = line.split(" ") u = int(u) i = int(i) user_ratings[u].add(i) return user_ratings #获取测试集的评分矩阵 def load_test_data(self, path): file = open(path, 'r') for line in file: line = line.split(' ') user = int(line[0]) item = int(line[1]) self.test_data[user - 1][item - 1] = 1 def train(self, user_ratings_train): for user in range(self.user_count): #随机获取一个用户 u = random.randint(1, self.user_count) #训练集和测试集的用于不是全都一样的,比如train有948,而test最大为943 if u not in user_ratings_train.keys(): continue # 从用户的U-I中随机选取1个Item i = random.sample(user_ratings_train[u], 1)[0] # 随机选取一个用户u没有评分的项目 j = random.randint(1, self.item_count) while j in user_ratings_train[u]: j = random.randint(1, self.item_count) #python中的取值从0开始 u = u - 1 i = i - 1 j = j - 1 #BPR r_ui = np.dot(self.U[u], self.V[i].T) + self.biasV[i] r_uj = np.dot(self.U[u], self.V[j].T) + self.biasV[j] r_uij = r_ui - r_uj loss_func = -1.0 / (1 + np.exp(r_uij)) # 更新2个矩阵 self.U[u] += -self.lr * (loss_func * (self.V[i] - self.V[j]) + self.reg * self.U[u]) self.V[i] += -self.lr * (loss_func * self.U[u] + self.reg * self.V[i]) self.V[j] += -self.lr * (loss_func * (-self.U[u]) + self.reg * self.V[j]) # 更新偏置项 self.biasV[i] += -self.lr * (loss_func + self.reg * self.biasV[i]) self.biasV[j] += -self.lr * (-loss_func + self.reg * self.biasV[j]) def predict(self, user, item): predict = np.mat(user) * np.mat(item.T) return predict #主函数 def main(self): #获取U-I的{1:{2,5,1,2}....}数据 user_ratings_train = self.load_data(self.train_data_path) #获取测试集的评分矩阵 self.load_test_data(self.test_data_path) #将test_data矩阵拍平 for u in range(self.user_count): for item in range(self.item_count): if int(self.test_data[u][item]) == 1: self.test[u * self.item_count + item] = 1 else: self.test[u * self.item_count + item] = 0 #训练 for i in range(self.train_count): self.train(user_ratings_train)#训练1000次完成 predict_matrix = self.predict(self.U, self.V) #将训练完成的矩阵內积 # 预测 self.predict_ = predict_matrix.getA().reshape(-1) #.getA()将自身矩阵变量转化为ndarray类型的变量 self.predict_ = pre_handel(user_ratings_train, self.predict_, self.item_count) auc_score = roc_auc_score(self.test, self.predict_) print('AUC:', auc_score) # Top-K evaluation scores.topK_scores(self.test, self.predict_, 5, self.user_count, self.item_count) def pre_handel(set, predict, item_count): # Ensure the recommendation cannot be positive items in the training set. for u in set.keys(): for j in set[u]: predict[(u - 1) * item_count + j - 1] = 0 return predict if __name__ == '__main__': #调用类的主函数 bpr = BPR() bpr.main() |
贝叶斯个性化排序运行结果查看

