跳转至

神经网络概述

从感知器说起

生物神经元

我们学习过生物,所以我们都可能比较熟悉生物意义上的神经元,也就是我们人脑内的那些,那么它是不是这个样子的呢:

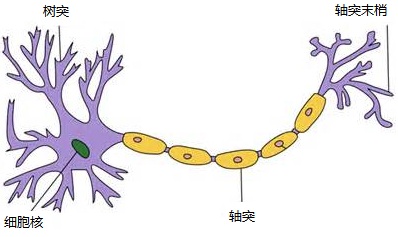
shengwu.png

其实,对于神经元的研究由来已久，1904年生物学家就已经知晓了神经元的组成结构。

一个神经元通常具有多个树突，主要用来接受传入信息；而轴突只有一条，轴突尾端有许多轴突末梢可以给其他多个神经元传递信息。轴突末梢跟其他神经元的树突产生连接，从而传递信号。这个连接的位置在生物学上叫做“突触”。

感知器

类比与我们人脑的神经元,人们发表了抽象的神经元模型---感知器/机,但后来感知器/机和神经元在本质上其实是相同的。只不过他们叫法的区别在于:我们说感知器的时候，它的激活函数是阶跃函数；而当我们说神经元时，激活函数往往选择为sigmoid函数或tanh函数。感知器算法在上个世纪50-70年代很流行，也成功解决了很多问题。并且，感知器算法也是非常简单的。

感知器的定义

下图是一个感知器/机：

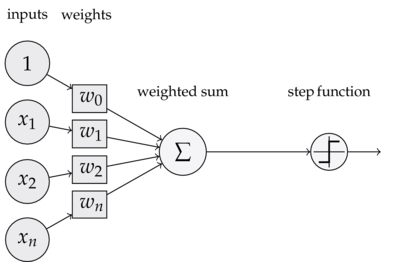
gzq.png

可以看到，一个感知器/机有如下组成部分：

  • 输入权值:一个感知器/机可以接收多个输入(x1,x2..xn),每个输入上有一个权值(w1,w2,wn),此外还有一个偏置项b，就是上图中的w0。

  • 激活函数:感知器/机的激活函数可以有很多选择,比如我们可以选择阶跃函数来作为激活函数。

  • 输出:感知器/机的输出由这个公式来计算:y=f(wx+b)

注意:鉴于感知器/机与神经元只是激活函数的不同,所以计算一个神经元的输出的方法和计算一个感知器的输出仍然是一样的。

(★补充)激活函数:

在神经元中，输入的 inputs 通过加权，求和后(也就是我们的输入权值的内容)，还被作用了一个函数，这个函数就是激活函数 Activation Function。

如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

一般有以下激活函数:

  1. sigmoid激活函数
  2. tanh激活函数
  3. Relu激活函数
  4. Leak Relu激活函数
  5. SoftPlus激活函数
  6. pReLU激活函数
  7. ELU激活函数
  8. maxout激活函数
  9. softmax激活函数
  10. log-softmax激活函数
  11. exp激活函数
  12. softplus激活函数

感知器还能做什么

它可以拟合任何的线性函数，任何线性分类或线性回归问题都可以用感知器来解决。

总结

  • 人工神经网络的神经元用传递函数对输入的线性加权进行非线性处理以产生输出；
  • 感知器是一种二分类的监督学习算法，通过自适应调整权重解决线性分类问题；
  • 感知器的神经元之间通过权重传递信息，权重的变化根据误差来进行调节；
  • 感知器不能解决以异或为代表的线性不可分问题。

神经网络

介绍

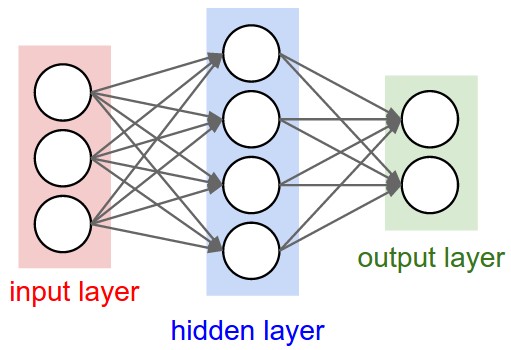
wl.png

神经网络其实就是按照一定规则连接起来的多个神经元(感知器)。上图展示了一个全连接(full connected, FC)神经网络，通过观察上面的图，我们可以发现它的规则包括：

  1. 神经元按照层来布局。最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的。
  2. 同一层的神经元之间没有连接。
  3. 第N层的每个神经元和第N-1层的所有神经元相连(这就是全连接的含义)，第N-1层神经元的输出就是第N层神经元的输入。
  4. 每个连接都有一个权值。

上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络，比如卷积神经网络(CNN)、循环神经网络(RNN)，他们都具有不同的连接规则。

注意:在本质上神经网络与多层感知器/机(Multi Layer Perceptron,即MLP)其实并无区别。

反向传播算法(BP)

(★补充)超参数: 我们可以说神经网络是一个模型，那么这些权值就是模型的参数，也就是模型要学习的东西。然而，一个神经网络的连接方式、网络的层数、每层的节点数这些参数，则不是学习出来的，而是人为事先设置的。对于这些人为设置的参数，我们称之为超参数(Hyper-Parameters)。

BP（Back-propagation，反向传播）神经网络是最传统的神经网络。

下面我们将以一个实例进行推导:

1.png
这里出现了超参数,即:以全连接,3层网络结构,每层2个节点构造了此模型。
2.png
3.png
4.png
5.png
6.png

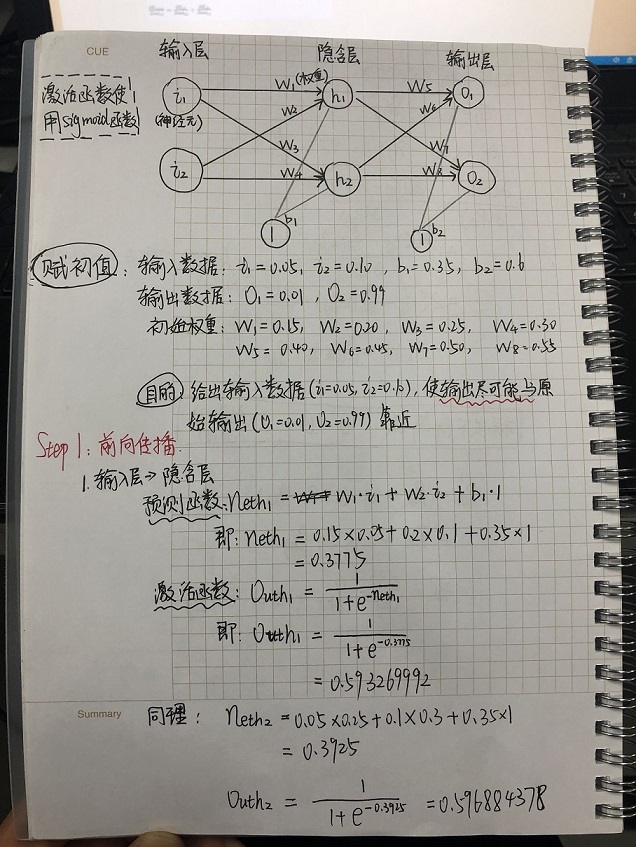
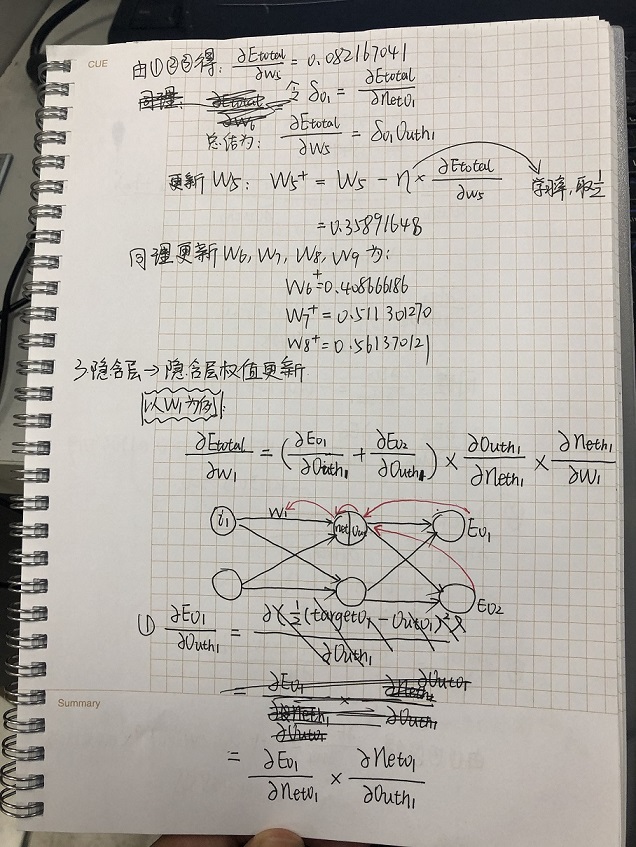
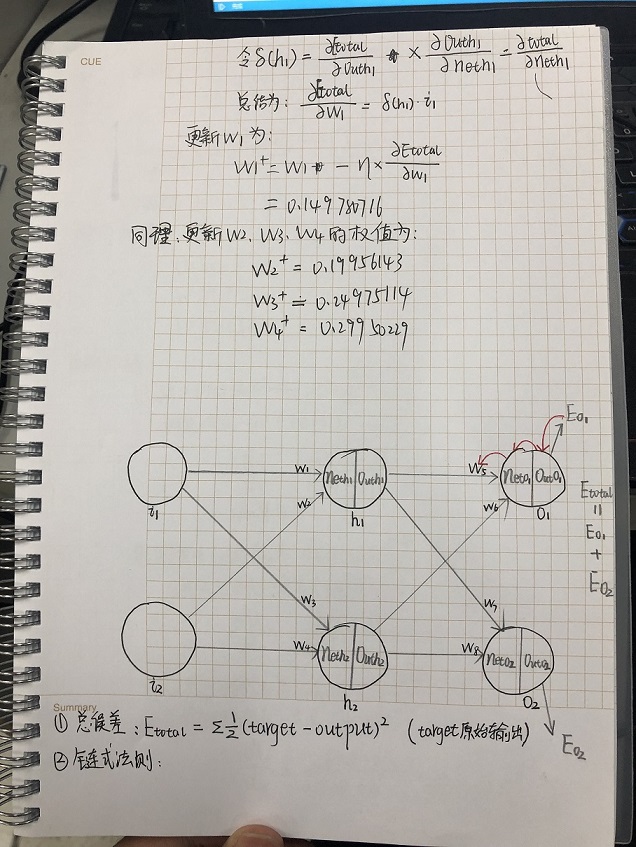
对于第5页的公式②,我在这里补充出了推导:

zm.png

至此，我们已经推导出了反向传播算法。需要注意的是，我们刚刚推导出的训练规则是根据激活函数是sigmoid函数、平方和误差、全连接网络、批量梯度下降优化算法。如果激活函数不同、误差计算方式不同、网络连接结构不同、优化算法不同，则具体的训练规则也会不一样。但是无论怎样，训练规则的推导方式都是一样的，应用链式求导法则进行推导即可。

ip2.png

向量化神经网络公式推导:下载